Выделение блоков фиксированных размеров
Рисунок 4.10. Выделение блоков фиксированных размеров
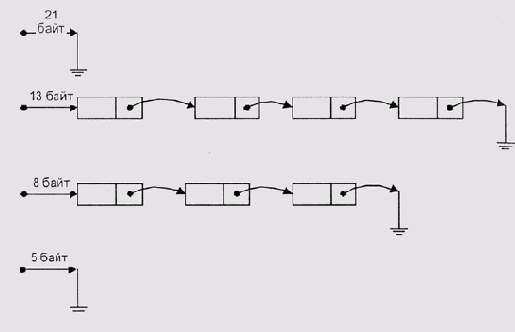
На практике, числа Фибоначчи не используются. Одной из причин, по-видимому, является относительная сложность вычисления такого Fi, которое не меньше требуемого размера блока. Другая причина — сложность объединения свободных блоков со смежными адресами в блок большего размера. Зато широкое применение нашел алгоритм, который ограничивает последовательные размеры блоков более простой зависимостью — степенями числа 2: 512 байт, 1 Кбайт, 2 Кбайт и т. д. Такая стратегия называется алгоритмом близнецов (Рисунок 4.11).
Одно из преимуществ этого метода состоит в простоте объединения блоков при их освобождении. Адрес блока-близнеца получается простым инвертированием соответствующего бита в адресе нашего блока. Нужно только проверить, свободен ли этот близнец. Если он свободен, то мы объединяем братьев в блок вдвое большего размера, и т. д. Даже в наихудшем случае время поиска не превышает О (log(Smax)-log(Smin)), где Smax и Smin обозначают, соответственно, максимальный и минимальный размеры используемых блоков. Это делает алгоритм близнецов трудно заменимым для ситуаций, в которых необходимо гарантированное время реакции — например, для
задач реального времени. Часто этот алгоритм или его варианты используются для выделения памяти внутри ядра ОС.